Understanding primary school teachers’ mathematical knowledge for teaching

There is growing evidence for the importance of developing strong foundational skills in mathematics at the start of primary school. Studies have shown the predictiveness of early numeracy skills for increasing later reading and mathematics scores (Platas et al., 2022; Duncan et al., 2007), as well as the link between early mathematics skills and later outcomes, such as high school graduation and earning potential (Hanushek & Woessmann, 2008). Considering this increasing body of knowledge, governments around the world are beginning to focus attention on the quality of instruction and learning in primary mathematics classrooms (Sitabkhan & Platas, 2018).

Recent research has also pointed to the crucial role of teacher knowledge in improving student outcomes. In math, there is a specialized type of teacher knowledge, known as mathematical knowledge for teaching (MKT), which is key for high-quality instruction (Loewenberg Ball et al., 2008; Baumert et al., 2010; Mosvold, 2022; Senk et al., 2012). MKT consists of what teachers need to know about mathematical content and how students learn that content, to teach math effectively. For example, consider place value, which is a foundational topic in early mathematics. First, teachers themselves must have flexible and deep knowledge about the place value system. Further, they should know which types of problems, models, and manipulatives to use to introduce place value concepts to students. They should also be familiar with the typical errors that students make, as well as the steps to remedy different types of errors. Lastly, they should know when to move students from concrete to abstracted understandings of the place value system. Without all this knowledge, teachers would be limited in their ability to teach place value effectively to their students.

Primary school teachers in many low- and middle-income countries often struggle with teaching math. We know that many primary teachers in these contexts often receive inadequate training in mathematics instruction (Hoppers et al., 2009; Haßler et al., 2019), and many studies show that teachers themselves cannot solve basic math problems (Bold et al., 2017; Brunetti et al., 2020). However, missing in all this evidence are systematic data that can help governments and implementers identify specific strengths and weaknesses in teacher knowledge. We need to be able to better target training and support to areas where teachers most need it, answering questions such as, In what domains do teachers struggle with the content itself? In what domains do teachers need more knowledge on how students learn? In what domains do teachers need support with identifying appropriate problems for their students?

In this paper, we present an exploratory study that strove to answer these questions. This study took place as part of the US Agency for International Development (USAID)–funded Okuu Keremet! Program in the Kyrgyz Republic, which was conducting a pilot study of a primary school mathematics intervention. The goal of the pilot study was to test an approach to improving the quality of instruction in grade 1–4 math classrooms. The piloted intervention provided a professional development package to teachers, including sample lesson plans to use in the classroom, training on new pedagogical techniques, and in-classroom support by a coach. As part of the pilot evaluation, we used a survey specifically targeting early primary mathematical knowledge for teaching, the Foundational MKT (FMKT) to understand what teachers learned about mathematics teaching and learning and provide concrete recommendations for future iterations of the mathematics intervention (the FMKT survey can be found at https://doi.org/10.5281/zenodo.13356550).

We present illustrative results of the FMKT survey by showing changes we detected between baseline and endline, and then highlighting elements of the intervention related to these changes (e.g., content in teacher training sessions and/or materials provided to teachers). We reflect on how conducting a direct teacher assessment of knowledge added value to the pilot study.

Before this intervention, the government in the Kyrgyz Republic expressed interest in using instructional strategies that build critical thinking and problem-solving skills in the classroom. However, research is lacking within the Kyrgyz Republic on how students are learning mathematics, what current instruction looks like, and how effective preservice education is. Large-scale student assessments using the National Sample-Based Assessment of Students’ Educational Achievement (NOODU), which assessed students in grade 4 in 2017, are available (Valkova et al., 2018). NOODU took a snapshot of what students know and can do as measured against the national curriculum. The results showed that only 40 percent of students reached the appropriate proficiency level to start secondary school mathematics, suggesting the need for improved quality of instruction in primary school mathematics. Kazakbaeva (2023) additionally points to a lack of resources and training for Kyrgyz teachers across all subjects and suggests that teachers need more support to enact new curricular reforms.

We posit that understanding what teachers know and where gaps in their knowledge are may provide a clear direction for government reforms seeking to improve instruction. By using the FMKT, we are able to understand better the areas in which our intervention supported teachers’ MKT and identify gaps in the intervention that would inform future iterations.

We structure the results section of this paper according to our core research questions:

• In what ways did the FMKT survey identify areas in which the intervention was successful, and point to ongoing challenges?

• What elements of the intervention present opportunities to understand these successes and challenges?

Within the field of teacher professional development, researchers have long sought to identify the knowledge, skills, and attitudes teachers need to successfully support strong student learning outcomes (Shulman, 1987). Early research and theory on teacher knowledge predominantly focused on teachers’ general knowledge. In his groundbreaking work exploring teacher knowledge, Shulman (1987) identified seven categories of knowledge. The first four categories connected to general teacher knowledge, such as pedagogy, knowledge of students, context, and purpose. The last three categories related to knowledge of the subject, including content knowledge, pedagogical content knowledge, and knowledge of the curriculum. Content knowledge refers to the depth of knowledge that a teacher has about the subject itself—for example, their procedural knowledge and conceptual understanding of mathematics topics, as well as of the connections between topics. Pedagogical content knowledge refers to the specialized knowledge teachers have about the ways children learn and can be supported to understand particular topics—for example, teachers need to recognize when and how manipulatives are likely to help students understand a concept better (Carbonneau et al., 2013) While other researchers have presented variations in general categories of knowledge, most overlap in identifying content knowledge and pedagogical content knowledge as core subject-specific knowledge teachers must have to be successful (Shing et al., 2015).

In 2008, Loewenberg Ball and colleagues endeavored to further unpack this subject-specific knowledge in the case of mathematics to identify more explicitly the content-related knowledge and skills teachers need to develop for successful primary mathematics instruction (Loewenberg Ball et al., 2008). Through their research, they identified six categories of knowledge that teachers need, which they refer to as Mathematical Knowledge for Teaching (MKT), and which together span Shulman’s content, pedagogical content, and curriculum categories. Acknowledging that the boundaries between subject knowledge categories could be fuzzy, Loewenberg Ball and colleagues’ MKT model differentiated common mathematics knowledge that teachers might share with most people from specialized mathematics knowledge that teachers need, such as the understanding of connections between mathematics domains. Under pedagogical content knowledge, the MKT model delineates the understanding teachers must have of how children learn mathematics (such as typical learning progressions in the development of algebraic thinking), the tools and methods most useful for supporting children in their learning (such as which representations support the development of algebraic thinking), and an understanding of curricular connections. As for previous researchers endeavoring to understand teacher knowledge, the ultimate goal of unpacking mathematical knowledge for teaching is to identify what mathematics teachers need to know to ensure student learning, so that teacher professional development can support teachers in developing and applying this knowledge effectively.

From the same body of research through which Loewenberg Ball and colleagues (2008) were able to elucidate the MKT model, the same group of researchers also developed the MKT Measures (MTK-M)—an instrument that could be used to diagnose and build teachers’ MKT through use in professional development settings (Hill et al., 2004). The MKT-M consists of items that focus on teachers’ knowledge in three areas: (1) mathematics content; (2) how mathematics develops among learners; and (3) how to best support student learning. Platas (2014) developed similar measures for preschool math knowledge. The Knowledge of Mathematical Development Survey measures teachers’ knowledge of developmental progressions in learning (e.g., which arrangements of objects are the easiest for children to count, a row or a circle?) (Platas, 2014).

Loewenberg Ball et al. (2008) and others have acknowledged that the items developed are likely culturally bound. Because of this, researchers in other contexts have explored adapting the same items or developing items that are based on the theory underlying MKT and the MKT-M. This has included MKT instruments adapted and used in low- and middle-income contexts, such as Ghana (Cole, 2012) Indonesia (Ng, 2012), and Malawi (Jakobsen et al., 2018). In Malawi, Jakobsen and colleagues (2018) adapted the MKT-M to measure learning of preservice teachers. They selected items, adapted them to the Malawian context, and then conducted a deeper adaptation to ensure items were relevant to the school cultural context in Malawi (Delaney et al., 2008).

A missing component of these prior measures is a focus on early grades mathematics. The MKT-M measures tend to focus on upper primary math and are often too complex for teachers, even with the lengthy adaptations described previously. The Knowledge of Mathematical Development Survey, while easy for teachers to understand, is too focused on preprimary math and thus does not meet the need for early primary grades. To fill this gap, we developed and used the FMKT to evaluate a pilot of an educational intervention in the Kyrgyz Republic.

The FMKT tool was developed by some of the authors of the present paper to diagnose primary teachers’ MKT in global settings, aiming to create an open-source survey that could be adapted to new contexts and different purposes. The tool consists of 23 questions across various domains and item types. To develop items, we were guided by the Global Proficiency Framework for Mathematics (USAID et al., n.d.), as well as other global standards and curriculums that delineate what students should learn during the first 3 years of primary school (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010; Clements & Sarama, 2014). Items covered four core domains in early mathematics.

After drafting all items, we went through two phases of development. In Phase 1, we ground-truthed the survey with other mathematics experts from different countries (United States, The Kyrgyz Republic, South Africa, and Kenya), conducting five cognitive interviews. For Phase 2, we conducted a field test in Nepal consisting of cognitive interviews with 20 preservice teachers. After each phase, we revised the survey.

In this section, we present illustrative data from the baseline and endline administrations. We supplement certain findings with anecdotal evidence from the pilot intervention to understand what may have contributed to specific differences from baseline to endline.

In what ways did the FMKT survey identify areas in which the intervention was successful and point to ongoing challenges? What elements of the intervention present opportunities to understand these successes and challenges?

At baseline, teachers answered, on average, 56 percent of items correctly. By endline, teachers showed a statistically significant improvement of 7 percentage points, increasing the final average to 63 percent correct (t[600] = 6.01; P < 0.001) This represented approximately two more items solved correctly (out of 23) at endline.

To better understand the nature of this increase, we examined trends at the individual item level on the assessment. We found interesting trends in performance, particularly when focusing on: (1) “low score” items (i.e., items with low scores at both baseline and endline); or (2) “high gain” items (i.e., items with significant increases in performance from baseline to endline). These two types of items provide a picture of how the FMKT can be a useful tool to measure successes and challenges of an intervention.

Along with this analysis, we present examples of how elements of the intervention enabled or constrained shifts in teacher knowledge, which allowed us to identify successes and challenges of the pilot intervention.

Domain: Number Sense

Figure 1 displays teacher performance on the seven number-sense items. Items were given illustrative titles according to the content and number of items within that content area (e.g., “early math [1]” is the first early mathematics item; “early math [2]” is the second early mathematics item). There were significant, positive differences in performance on the decomposing numbers item and the two fraction items. The early math (1), early math (2), early math (3), and object grouping items showed very little movement from baseline to endline.

Figure 1

Teacher performance from baseline to endline on number sense items

* Increase was statistically significant (P < 0.05).

To explore this domain further, we provide detailed examples of a low score item (early math [2]) and a high gain item (decomposing numbers), subsequently.

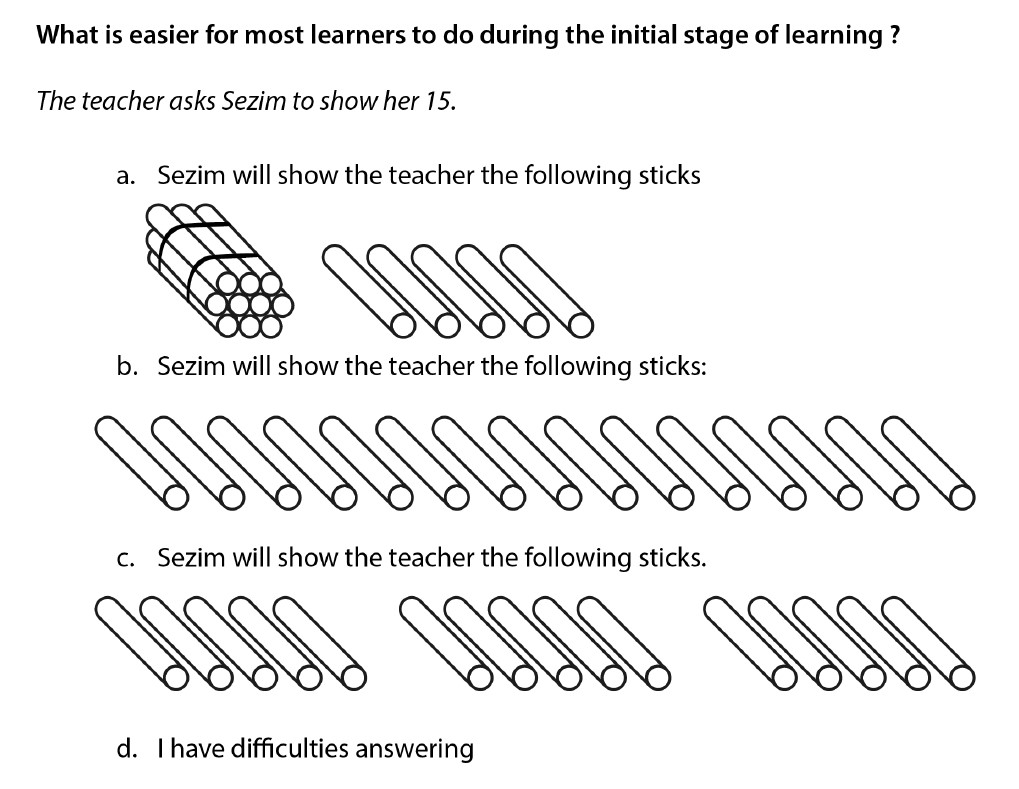
For the low score item, we show results for the early math (2) item (see Figure 2), which asked teachers about initial number concepts.

Figure 2

Early math (2) item

Figure 3 shows the distribution of answer choices.

Figure 3

Distribution of answers on early math (2) item

The correct answer for this item is B (by ones). The majority of teachers at baseline and endline chose A (by tens and ones). This represents a common misconception in early mathematics. Interestingly, more teachers chose A at endline than baseline, even after completing the pilot modules and receiving teacher training.

This may have occurred because many of the activities during trainings focused on teachers helping children to develop an understanding of place value but did not specifically address the issue of seeing numbers as “whole” before teaching students about place value. In fact, much of the training focused on place value by showing teachers how various tools such bundles, sticks, and place value blocks can support student understanding. Subsequent modules extensively used base-ten counters for addition and subtraction, emphasizing that students can use the counters to visualize two-digit numbers. In the trainings, teachers were asked to use base-ten counters to model numbers and operations. Therefore, the large amount of time dedicated to place value may have contributed to the scores on this item.

The decomposing numbers item, displayed in Figure 4, was a high gain item.

Figure 4

Decomposing numbers item

Figure 5 shows the distribution of responses to this item.

Figure 5

Distribution of answers on decomposing numbers item

The correct answer on this item is C (15 + 9). At endline, the proportion of teachers selecting option C nearly doubled, as compared with baseline (26 to 48 percent). Conversely, the number of teachers choosing B (3 + 2) was reduced by half (30 to 16 percent). This suggests that teachers gained knowledge of the decomposing (or “breaking apart”) strategy.

The intervention covered this strategy directly, allowing teachers ample time to learn and practice the strategy. Classroom observations conducted during the pilot also revealed that teachers were using this strategy in their lessons.

Domain: Operations

Figure 6 shows the percentage of teachers who responded correctly on the nine operations items at baseline and endline. On some items, such as strategy for addition (2) and equations, teachers performed well at both baseline and endline. On other items, such as strategy for addition (3) and errors in addition (2), teachers had low scores at baseline and endline. There were significant increases on three items: strategy for addition (2), errors in addition (2), and word problem—equations.

Figure 6

Teacher performance operations items

* Increase was statistically significant (P < 0.05).

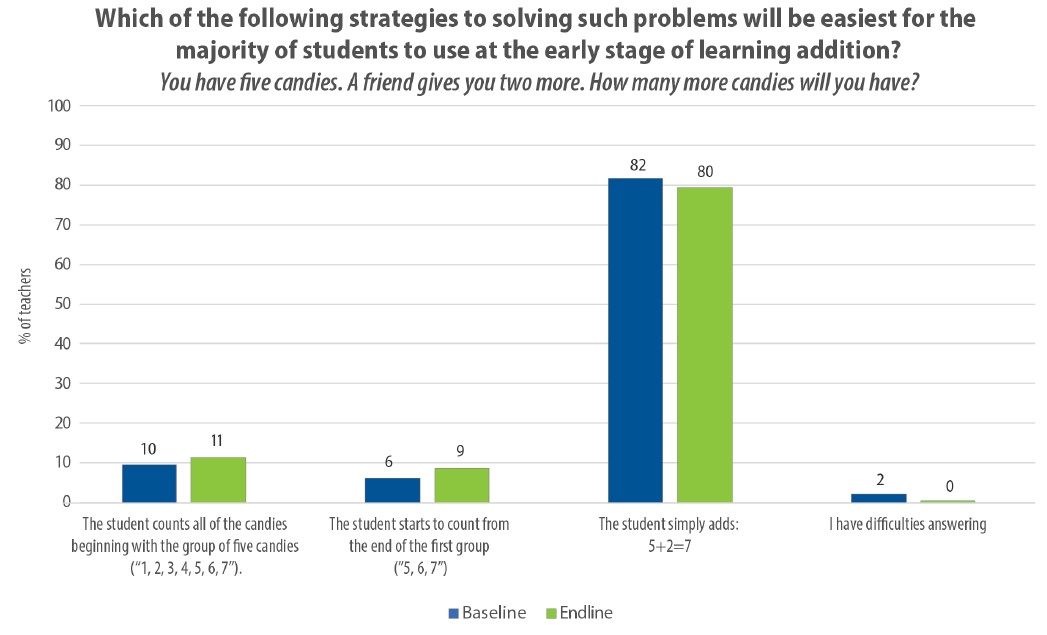
A low score item, strategy for addition (3), measured teachers’ knowledge of early mathematics strategies when students are just beginning to make sense of operations (see Figure 7).

Figure 7

Strategy for addition (3) item

Figure 8 displays the distribution of teacher answers for this item.

Figure 8

Distribution of answers for strategy for addition (3) item

The strategy for addition (3) item focused on progressions in children’s acquisition of addition concepts. For this item, the correct answer is A (student counts all candies). Counting on (answer B) and recall of a number fact (answer C) are both more complicated strategies that children develop over time.

As Figure 8 shows, only 10–11 percent of teachers chose A across baseline and endline, whereas approximately 80 percent chose C at both time points. This suggests that the intervention was not successful in supporting teachers’ knowledge of children’s initial development of certain concepts. This item and the early math item (see Figure 5) illustrate that initial math concepts continue to be an underdeveloped area in these teachers’ knowledge.

Although the training materials did briefly explain the progression of strategies for addition, all examples and practice time during training was dedicated to solving simple items using the break-apart method or automatic recall of number facts. This emphasis during the training may have contributed to the low scores initially and at endline on this item, as we saw on early number sense items.

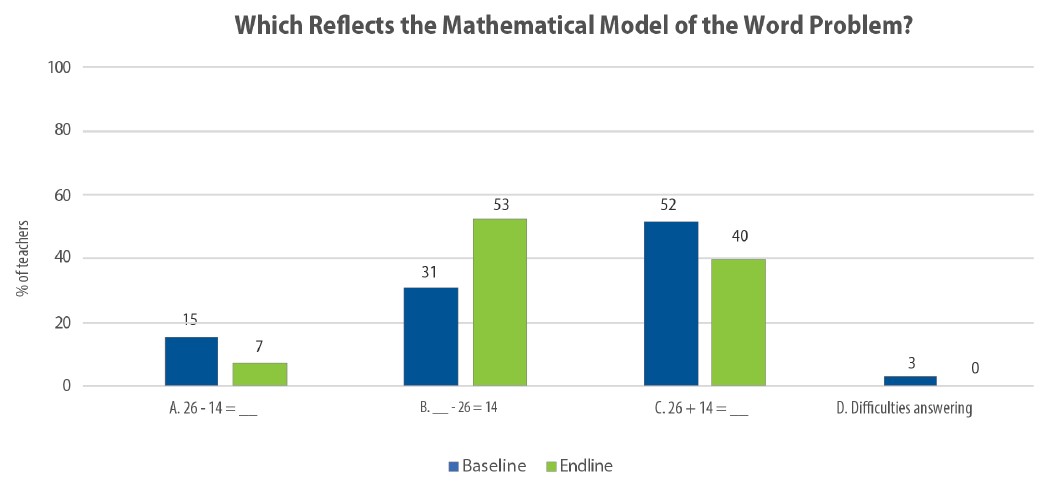
The word problem equations item, a high gain item, assessed teachers’ ability to create a mathematical model of a word problem (see Figure 9).

Figure 9

Word problem equations item

Figure 10 displays distribution of teacher answer choices.

Figure 10

Distribution of answers on word problem equations item

The correct answer for this item is B (___ - 26 = 14). At baseline, 31 percent of teachers chose the correct answer; at endline, 53 percent of teachers chose the correct answer, reflecting an increase in teacher knowledge. Importantly, the number of teachers who chose C (26 + 14), a common misconception, at endline was 40 percent, down from 53 percent at baseline.

The intervention paid specific attention to word problems and how to create mathematics models for problems. In the Kyrgyz Republic, it is common for teachers to create an equation of the solution of the word problem, not the mathematical model. Trainings encouraged teachers to create instead a mathematical model of the problem, providing the rationale behind why this supports student understanding. Teachers modeled how to do this during the training. The training also detailed common structures in word problems (see Carpenter et al., 1996). This explicit focus on different structures of word problems and their mathematical models may have helped teachers see patterns in the types of problems and their corresponding mathematical models, thereby contributing to the shifts seen from baseline to endline.

Domain: Geometry

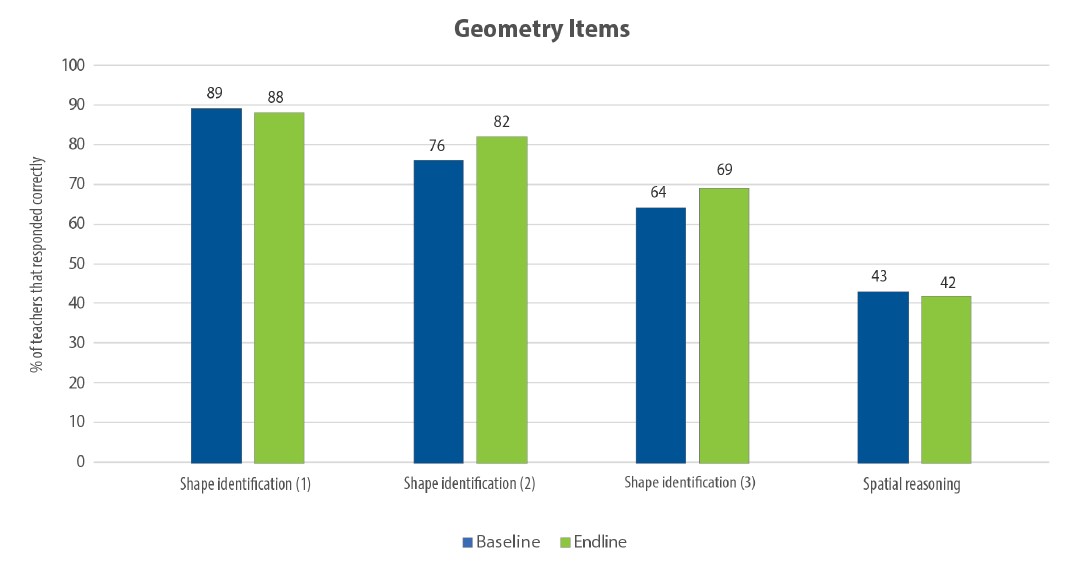
Although teachers’ performance varied on the geometry items, there were no significant increases for any item, nor were there items with very low scores (Figure 11).

Figure 11

Teacher performance from baseline to endline on geometry items

The lowest scoring item was spatial reasoning, but no change was seen from baseline to endline. Although the pilot included two modules focused on instructional techniques to help students understand the properties of geometry, little time was allocated for studying and practicing the material. This was partly because the geometry modules did not always match the curriculum calendars that teachers used. Because geometry was taught infrequently and at different times by different teachers, the timing of the trainings did not always match up to what teachers were doing in the classroom. Some teachers therefore had fewer opportunities to use and practice the lessons provided and did not receive the same amount of pedagogical support in the classroom as they received with numbers and operations. It could be that this lack of emphasis in the curriculum, which led to decreased time to practice the content, contributed to a lack of change in teacher knowledge from baseline to endline.

Domain: Measurement

Overall, teacher performance on measurement items was strong, as Figure 12 displays. For two of the three items (time and measuring length), teachers’ scores significantly improved from baseline to endline. There were no items with particularly low performance.

Figure 12

Teacher performance from baseline to endline on measurement items

* Increase was statistically significant (P < 0.05).

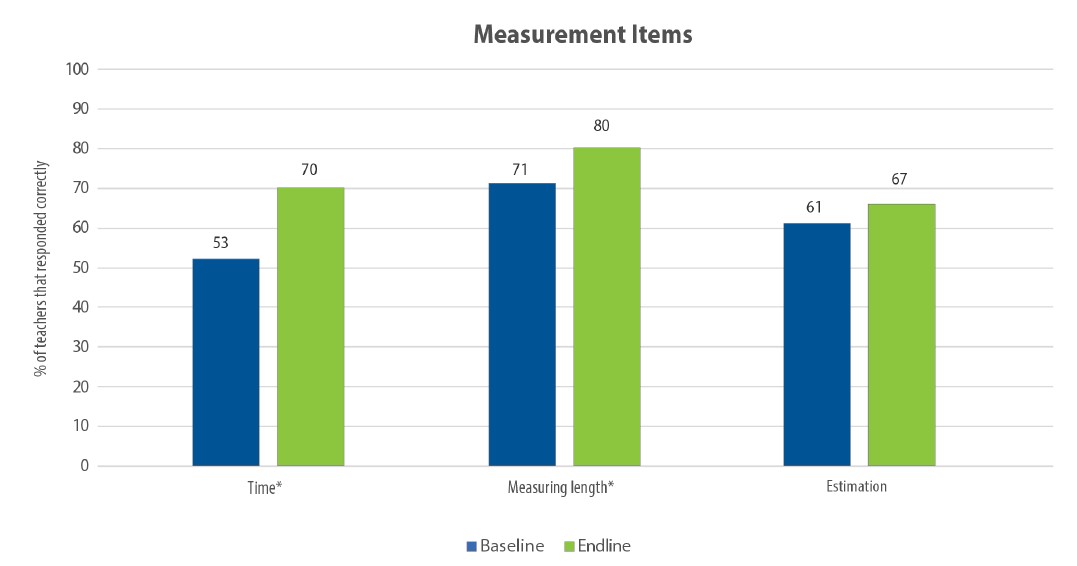
Figure 13 shows the item on time, a high gain item. The item asked teachers to choose the word item about elapsed time that would be easiest for students to solve when they first begin to learn about time.

Figure 13

Time item

Figure 14 displays distribution of teacher answer choices.

Figure 14

Distribution of answers on time item

Answer choice A (reading from 13:12 to 16:12) was the correct answer. At baseline, 53 percent of teachers chose the correct answer, while 24 percent chose C (reading from 13:16 to 13:32). At endline, 70 percent of teachers chose A (with reductions in all three of the other options).

To better understand how the pilot may have supported this shift in knowledge of measurement, we analyzed how the modules and training focused on enhanced teaching and learning of measurement. Historically, measurement was integrated with other domains in nearly all lessons in textbooks. For example, a lesson on two-digit addition would contain word problems related to measurement as a real-life application. Teachers were therefore very familiar with measurement but did not view it as a domain in and of itself, with properties and concepts that students needed to learn. In the modules, we treated measurement as a domain and shared information on how students learn measurement skills and concepts, as well as typical trajectories for learning. This shift may have led to the improved performance on measurement items in the FMKT survey.

The FMKT survey provided in-depth, detailed results on what teachers learned through the pilot intervention. The changes in scores we detected informed future iterations of the intervention. In addition, we were able to identify elements of the teacher training and the modules that may have been related to the differences in teacher performance we saw. The FMKT provided us illustrations of the successes of the intervention and identified areas for growth.

Areas of success included teachers being more able to identify strategies for basic operations and create mathematical models of word problems. Teachers showed growth on understanding learning progressions within the domain of measurement, such as understanding learning trajectories for elapsed time.

Areas for growth included foundational learning topics such as counting, basic addition, and geometry. We found that teachers performed worse on FMKT items measuring foundational topics at endline than at baseline. Closer examination of the intervention suggested that the training may have inadvertently reinforced misconceptions about developmental trajectories in early learning. A strong focus on place value was initially deemed important during the design of the intervention, but the FMKT provided us with insight that emphasizing the importance of place value without ensuring that teachers understood how place value concepts fit into overall number development may not have supported teacher knowledge development. In geometry, we found no change from baseline to endline. Although we learned that existing geometry knowledge was strong, there was room to grow within other areas of geometry, such as spatial awareness. However, we did not see this growth.

Overall, the FMKT provided us with actionable next steps for revising the intervention. This study confirms the centrality of MKT to improving the quality of instruction and, like other studies on the importance of MKT, contributes insights from a case study in a new context in which MKT has not been used previously.

This work with teacher knowledge follows the trend from the past 20 years of focusing on student learning outcomes. As a result of the Millennium Development Goals in 2000, the international community began a discussion about early grade student learning: How do we know where students are in terms of learning outcomes? Are students learning what they should learn by the end of an intervention? The Early Grade Reading Assessment (EGRA), Early Grade Mathematics Assessment (EGMA), Annual Status of Education Report (ASER) and other assessments were developed to help governments and implementers understand the impact of reading and math interventions on student learning outcomes. With foundational literacy and numeracy emerging as a global priority at the 2022 UN Transforming Education Summit, we believe that the momentum needs to shift toward helping teachers improve their practice and that this study illustrates how to make this shift.

When we began the work in the Kyrgyz Republic, the pilot intervention resembled many of the interventions developed globally and funded by large donors. It consisted of development of materials, teacher training, and extra support provided to teachers. The only measurement planned was student learning outcomes. We decided this was not enough to measure intervention success, and that in addition to measuring student learning outcomes, we should measure the direct focus of the intervention: developing teacher knowledge. By measuring development of teacher knowledge, we elevated its status within the project and in the Kyrgyz Republic, where this focus had not existed before. MKT became important because we measured it. MKT was a topic of discussion at project meetings, at teacher trainings, and at meetings with the donor. Results of the pilot intervention were interpreted by project staff and the donor using MKT as a lens. The FMKT enabled us to have these conversations, providing easily interpretable evidence around the types of knowledge teachers were or were not developing.

By centering and measuring teacher knowledge, we were able to show how to collect specific and actionable information to target support to teachers. We hope this study provides an example for how to expand measurement of impact on traditional interventions to include teacher learning outcomes—much like studies using the EGRA, EMGA and ASER did for student learning outcomes. To be clear, we are not advocating for the FMKT, or other surveys that measure teacher knowledge, to be used for high-stakes testing. Measuring teacher knowledge has clear pedagogical benefits; using teacher knowledge as a system-level tool for assessing teachers is controversial and without strong evidence. Teacher knowledge measures should be used instead to support teacher growth and target interventions appropriately.

Finally, we reflect on an unexpected use of the FMKT that surfaced during the adaptation of the survey items in the Kyrgyz Republic. During the adaptation workshop, we found ourselves spending ample time discussing each item, as well as the multiple answer choices, each of which represented a common error in mathematical knowledge. Through this detailed discussion, all participants built new MKT, both for the team in the Kyrgyz Republic, who were able to delve more into the evidence base of how students learn math, and for the international-based team, who were able to learn more about how math is taught in the Kyrgyz Republic. This rich dialog leads us to believe that the individual items on the MKT survey may also be useful as a professional development tool to use with teachers to build their knowledge. More work is needed in this area to understand how these items may be used as part of a professional development program.

The data supporting the current study are available from the authors upon reasonable request.

We are thankful for the participation of the primary school teachers in the Kyrgyz Republic, who are always striving to improve their practice. This study would not have been possible without the support of the Okuu Keremet! team and the math working group members. Their participation to help digitize the FMKT, organize training workshops, and provide translation services were invaluable.

The development of the FMKT survey was funded by RTI International through an internal research and development award focused on supporting teachers in early mathematics.

RTI Press Associate Editor: Michael Willoughby